Using repl.it to Code
Trigonometry
Sidenote: This
dips into quite a bit of mathematics. This gives a basic tutorial on trigonometry. You may not have learned that
yet, so feel free to skip this section.
If you haven't learned trig yet, this may not make much sense. In short, for a given right triangle, if you have an angle and the length of a side, you can find the length of another side. Or if you have two sides, you can find an angle. First a little math lesson before we get back to the Math object.
Theta (θ) is the angle we're looking at. Side x is called the adjacent to the
angle. Side y is opposite the angle. Side h is the hypotenuse.
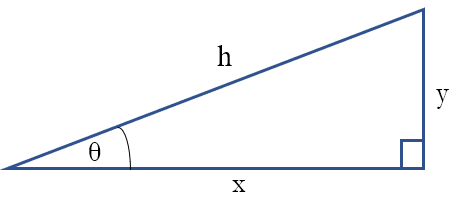
We can use sine (sin), cosine (cos), and tangent (tan) to find any piece we're missing if we have two other values. All three of these trig functions use the angle and two sides.
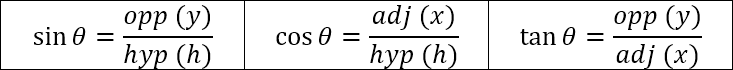
If you have an angle of 30° and an adjacent of 15, you can figure out the opposite using tangent (or the hypotenuse using cosine). We use this to figure out high rockets fly. We know how far away from the base we are and we can measure the angle of ascent. With some trigonometry using tangent, we can calculate how high the rockets go.
That's all nice and good, but what on Earth is the tangent of 30°?
This is where the Math object helps us out. There is one slight complication though. The Math object does not use degrees! It measures angles in radians. A radian is a circle that has an arc equal to its radius. An entire circle encompasses 360°, which is 2π radians. Any time we want to use trig in degrees, you have to convert the angle one way or the other.
The formulas are:
- angleInDegrees * Math.PI / 180; //gives radians
- angleInRadians * 180 / Math.PI; //gives degrees
So, to get that tan of 30°, you need this.
- Math.tan(30 * Math.PI / 180);
Let's see how high that rocket went. If we were 15 meters (almost 50 feet) away from the launch pad and we measured an angle of 30°...
- let adjacent = 15;
- let degree = 30;
- let radian = degree * Math.PI / 180; //0.5235987755
- let tangent = Math.tan(radian); //0.5773502691
- let opposite = tangent * adjacent; //8.6602540378
The opposite represents how high up it went, so 8.66 meters, which is about 28 feet!
The basic trig functions are:
- Math.sin()
- Math.cos()
- Math.tan()
But what if you have two sides and you need to get the angle? Using any of the formulas, you'd get some number
equal to sin θ or cos θ or tan θ. How do you get θ?
You would have to use the inverse of the trig functions, which I call the "arcs": arcsine, arccosine, and arctangent.
- Math.asin()
- Math.acos()
- Math.atan()
Let's work that last rocket question backwards.
- let adjacent = 15;
- let opposite = 8.66;
- let tangent = opposite / adjacent; //0.57733333333
- let radian = Math.atan(tangent); //0.52358607361
- let degree = radian * 180 / Math.PI; //29.9992722298
I used the same situation and just worked backwards and look… we got the same angle! It's different because of some
rounding, but 29.999° is really 30°, isn't it?
- Math.round(29.999); //30!! Yay!
There's even more to the Math object than that but they're rather specific and intended for upper level math stuff.
Search it out if you're interested!
JavaScript Math
Object